Pilots are taught to take off and land into the wind, and avoid landing or departing with a tailwind. There is a reason: The performance penalty of a tailwind is much greater than the benefit of a headwind. How big a penalty? Go to your POH and calculate it. The most common figure is to add 10 percent to the takeoff or landing roll for every two knots of tailwind up to 10 knots. The specific penalty will vary based on a number of factors like runway surface, density altitude, and gross weight. Somewhere down in the fine print, you may see an additional penalty for runway slope. But often runway slope is neglected, because most runways are level.
The paper exercise of calculating the effect of tailwinds on landing and takeoff distances is usually enough to convince pilots to avoid them. There is nothing like the experience of eating runway because of tailwinds. Eventually, whether through lots of calculations or direct experience, pilots gain the judgment to know how much tailwind penalty is acceptable given runway lengths, loads, obstacles and other factors like runway surface.
One factor that actually makes it fairly reasonable to accept a tailwind is downhill runway slope. Even then, the slope can be exasperating because runways like these are usually situated with other constraints, like hills, trees, cliffs and canyons, which can often make a sloping strip a one-way-in and one-way-out affair. In these cases, you have to live with the winds as they are and decide whether or not to accept them.
If the winds are such that you are considering taking off uphill, you will have to consider the effect on uphill takeoff performance. At a relatively low slope, POH advice and rules of thumb will hold true, but as steepness increases, the advice and rules of thumb break down. There is actually a point of no return where the steepness of a runway will exceed the excess thrust required to accelerate to takeoff speed. Unless there is a hurricane-force wind blowing downhill, you won’t take off.
A Legitimate Excuse
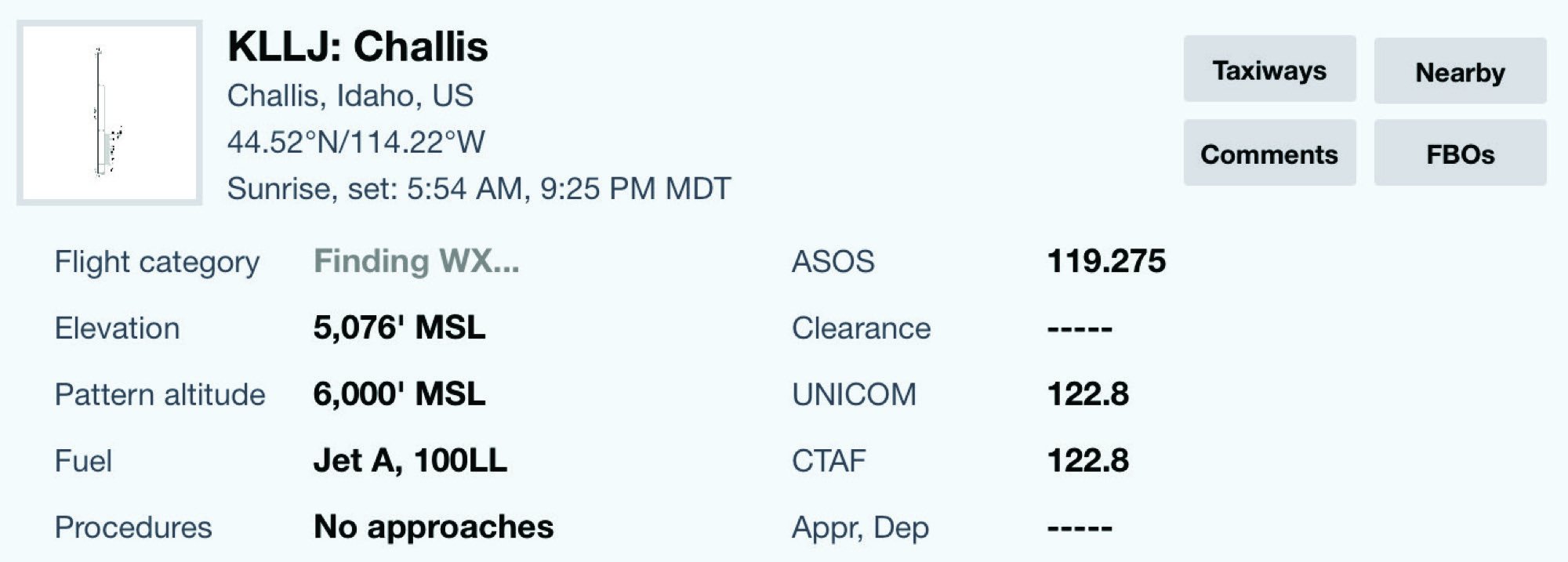
My first experience with runway slope came in Challis, Idaho. The 4600-foot-long runway is excessive by Kansas standards, but at 5076 feet msl, it is actually equivalent to the 2800-foot runway I learned to fly on there. I say equivalent because, based on the Koch chart for calculating aircraft performance at density altitude and assuming standard temperature in the following cases, a 1000-foot ground roll at sea level would require a 1200 feet at 1000 feet elevation, and 2000 feet at 5000 feet elevation. So a 1200-foot takeoff roll on a 2800-foot-long Kansas runway is 2.33 times the runway length. The same is true for the 2000-foot takeoff roll on the 4600 feet of runway at Challis. (In reality, the climb rate out of Challis would also be less, but in terms of runway requirements, they are virtually equivalent.)
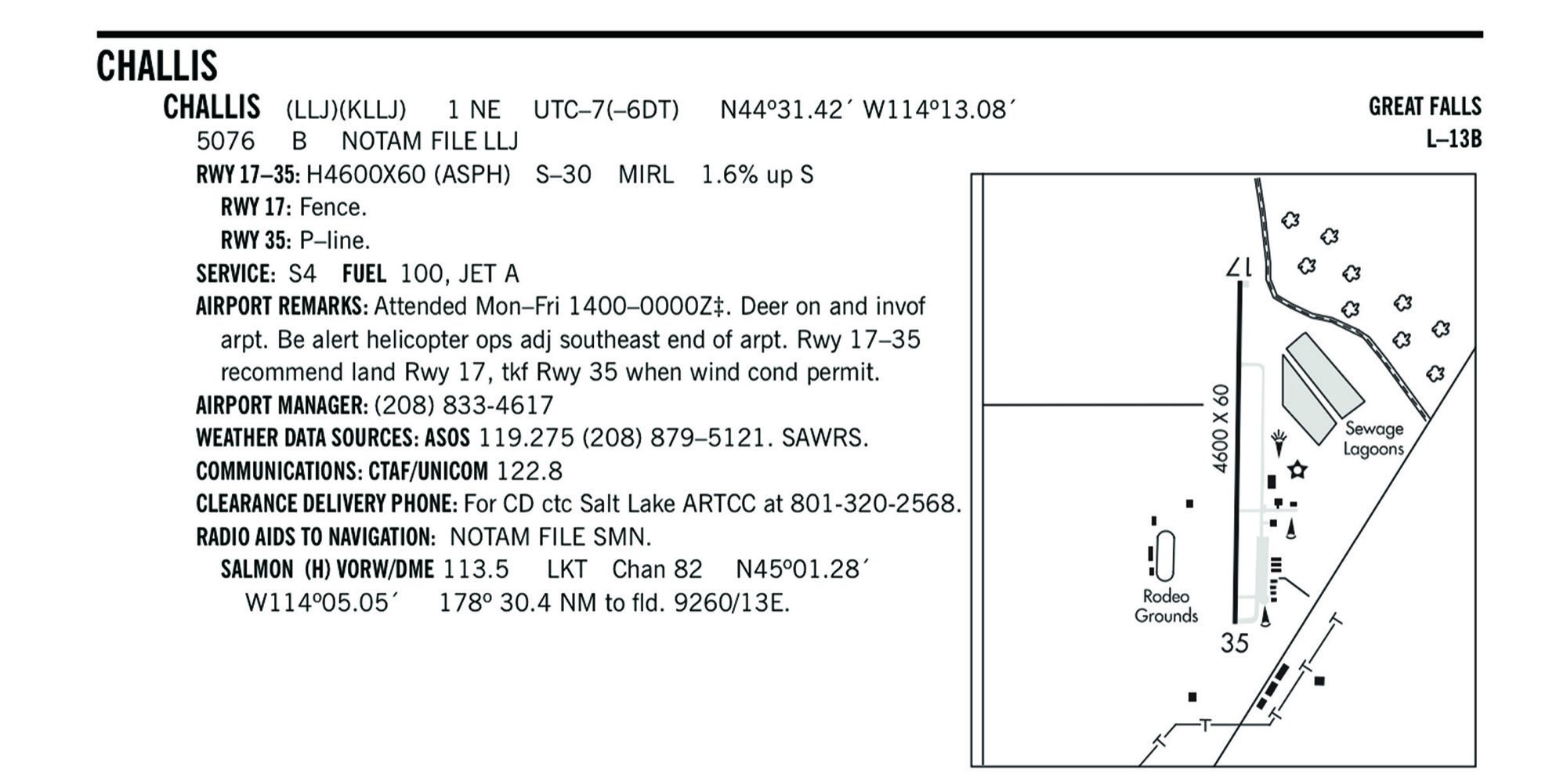
While the two runways seem equivalent—even down to the pavement—they have one major difference that changes everything for takeoff and landing operations. Much like the state itself, my hometown runway in Kansas is flat with the same elevation at both ends. In contrast, the north end touchdown point of the Challis runway is at 5004 feet msl while the south end is at 5076 feet. The Chart Supplement states that unless winds dictate otherwise, you land uphill on Runway 17 and take off downhill from Runway 35. It mentions the uphill slope to the south, although if you aren’t looking for it, you might not see the note.
The formula for calculating runway percent is the rise divided by the run times 100, so for Challis, it is a 1.6 percent grade. To the naked eye, the 72-foot difference doesn’t seem very dramatic because it’s spread over 4600 feet. However, while it looks very gentle, the kinetic energy penalty or reward that is imposed by that slight slope is quite steep. Taking off uphill requires the energy for a standard takeoff roll; plus, if you use the entire runway, the kinetic energy equivalent of hauling your aircraft’s gross weight up to the top of a seven-story building. And if you depart uphill, you just might use the whole runway.
Any time you see runway notes recommending one-way operations, check for both runway slope and potential terrain or obstructions.
Calculating Slope’s Effect
Takeoff is always a multivariate problem that depends on aircraft loading, runway surface conditions and whether or not there are obstacles. It also depends on the amount of excess thrust you have available and, of course, the amount and direction of the wind. There are several ways of breaking it down.
The first is to check your pilot’s operating handbook (POH). Most POHs are silent about slope, but some may offer a caution. For example, the POH for the Diamond DA-40-180 says a two-percent grade can increase the takeoff distance by 10 percent and can affect takeoff roll by even more. Looking at non-POH references, there are various rules of thumb that suggest a one-percent slope will increase takeoff roll from 10 to 22 percent, and decrease landing rolls from three percent to seven. The benefit of landing uphill is less than the penalty for taking off uphill.
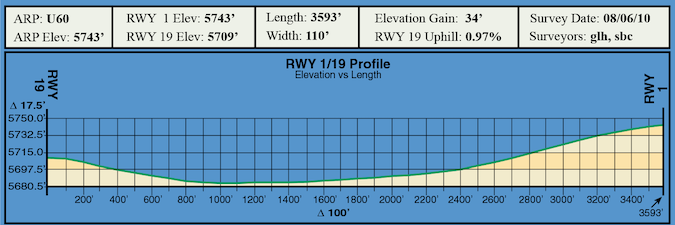
When I searched for a thorough discussion of slope and wind that offers rules of thumb, the most recent publication I found was Mountain, Canyon and Backcountry Flying, by Dr. Amy Hoover and Dick Williams, published in 2019. Dr. Hoover’s rule is that every one-percent change in slope changes the effective runway length by 10 percent. So the 1.6-percent slope of the 4600-foot-long Challis runway works out to be 736 feet longer (5336 feet) when taking off downhill or landing uphill and 736 feet shorter (3864 feet) when taking off uphill or landing downhill. This runway is not at all like my hometown runway in Kansas. The sidebar on the opposite page explores the mathematics of sloped runways in greater detail.
Trading Slope For Tailwind
Theoretically, there should be a nice inflection point where the reduction of your takeoff roll from the slope is equal to the amount a tailwind adds to your takeoff roll. Where is that point? It depends.
The rule of thumb for calculating the penalty for a tailwind typically stops at 10 knots. One reason is that until the aircraft accelerates faster than the tailwind, it can experience reverse controls, which is where the rudder, aileron and stabilizer inputs have the opposite result in terms of the direction they move the aircraft. Few pilots are able to handle this scenario skillfully, and it is particularly evil for tailwheel pilots. The greater the tailwind, the greater the exposure.
There is the critical factor of obstacles and geographic constraints for most downhill runways. Sloped one-way airstrips usually have significant terrain and obstruction factors constraining the departure. Wind from some directions could generate burbles or downdrafts. These additional factors likely are a part of your aeronautical decision-making as much as the trade-off of wind versus slope.
When wind and slope are near the inflection curve, there are enough other factors to consider that there is rarely a clear trade off.
Real-World Choices

When other local pilots and I depart from the 4600-foot-long Challis runway, we often accept as much as a 15-knot tailwind to depart downhill. We are encouraged by the slope, but we consider other factors as well, like the fact that most of the airport facilities are located at the south end, and the terrain to the north continues on downward over open fields. Taking off to the south is not only uphill, but is over the main part of town and toward rising terrain. In other words, even if the surrounding terrain was flat, we would likely accept a bit of tailwind just for convenience and safety.
In my experience, nearly every runway with a significant slope to consider has similar complex factors affecting the choice of uphill/downhill versus wind. When you are near the inflection point where wind and slope might take you beyond the effective runway length required for a safe takeoff, you can go to the POH and make a calculation, or can use the rule of thumb for calculating “effective runway length” with a tailwind.
But I will offer my own rule of thumb: Pay attention to any discomfort you might feel about the tradeoff between a sloped runway and a significant tailwind. If you simply aren’t comfortable making a decision, pitch your tent and wait. The slope will still be there in the morning, but the wind will eventually change to something with a bit less pucker.
Steepness Matters
If the 72-foot drop between the two runway ends at Challis was simply a vertical cliff rather than 4600 feet apart, an aircraft pushed off the top would hit the bottom at 67 feet per second, or 40 knots. Since that’s higher than a J3 Cub’s takeoff speed, if one was pushed off a 72-foot-high cliff, it could reach takeoff speed, theoretically. A runway with a slope acts like the old classic inclined plane problem from high school physics. Before your eyes glaze over, bear with me through a relatively quick review to better understand the effect of slope steepness.
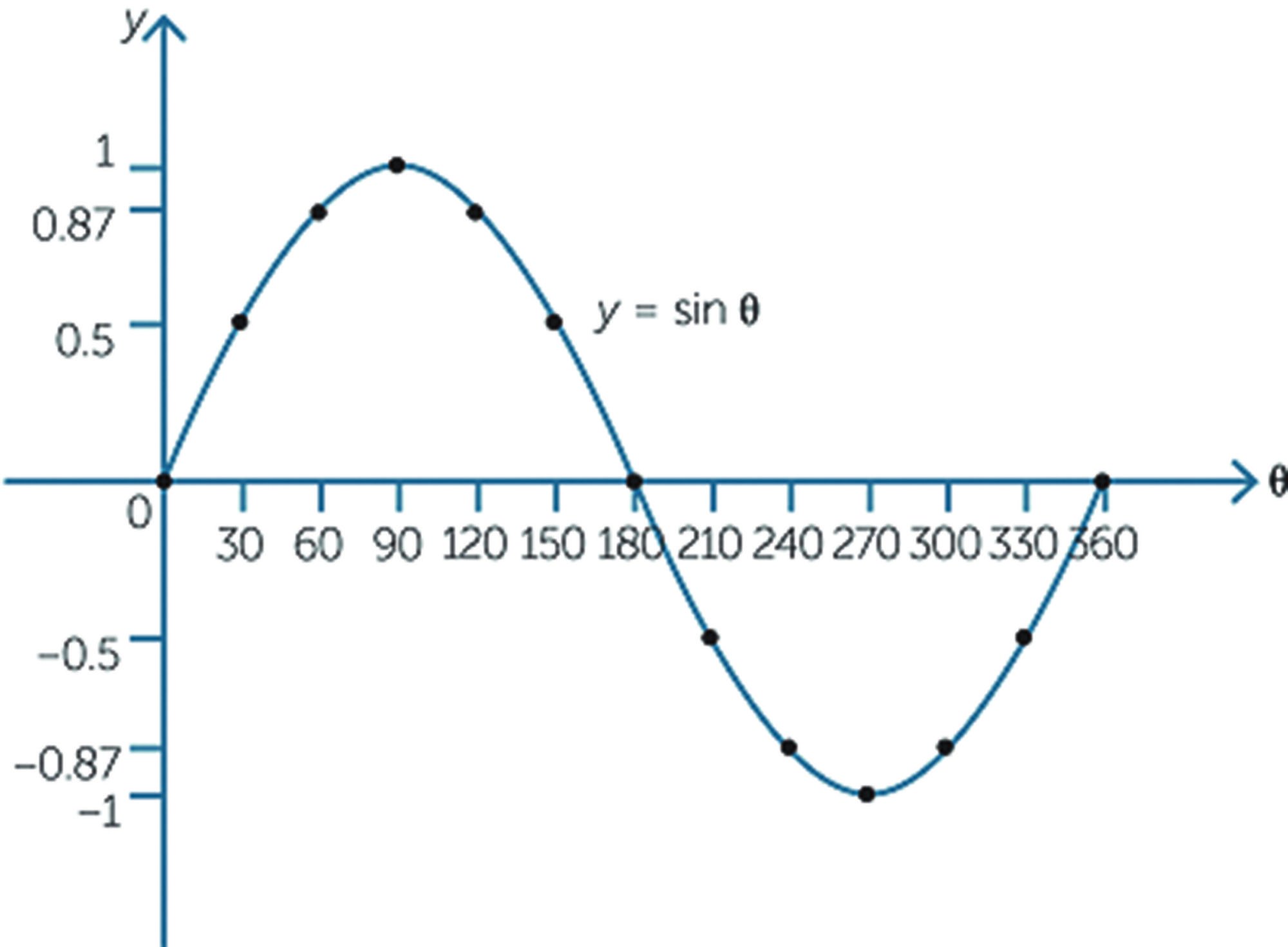
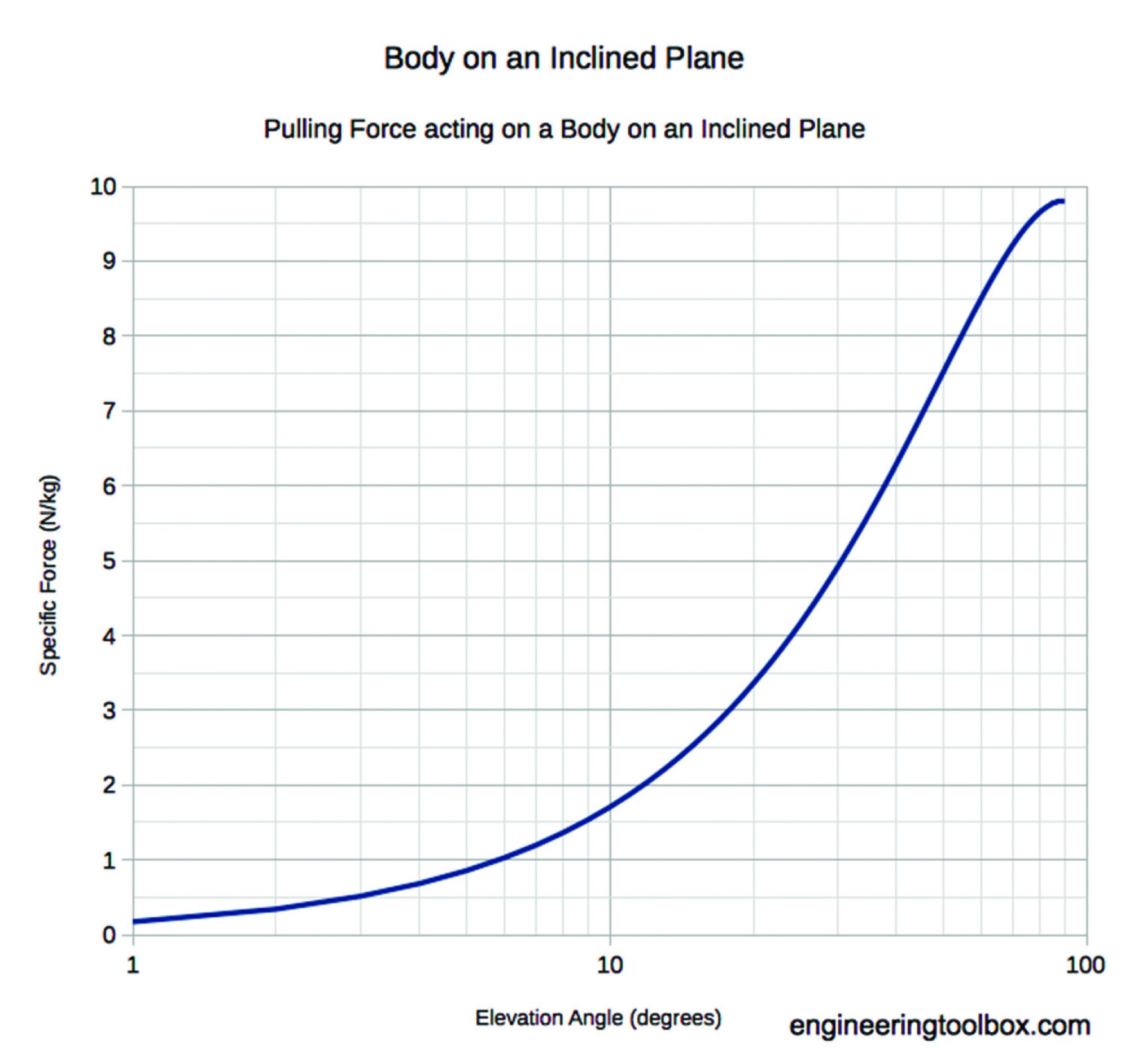
The physics formula for the speed gain from a fall (∆v) resulting from a height change of ∆ℎis ∆v=√2 g ∆ℎwhere g = the acceleration of gravity, which is 32 feet per second per second. The slope of the runway represents acceleration down an inclined plane. An aircraft sliding down an inclined plane will not accelerate like it was dropped off a cliff. Instead, its speed depends on the steepness of the angle. For runway slope, we only care about the sine of angles between 0 degrees and 90 degrees. The steeper the downhill angle, the larger the component of acceleration due to gravity. Looking at the sine curve in Graph A at right, you can see that a 30-degree angle has a sine value of 0.5 (yellow circles). At 60 degrees, the value is 0.87 (blue circles). This continues up to the point of a 90-degree vertical angle (essentially the cliff previously discussed) where the relationship is one-to-one or 1g acceleration (sine 90 degrees = 1).
The basic trigonometry of an inclined plane allows you to calculate the acceleration rate as the sine of the base angle. To do the math, you must first convert runway gradient from percent slope to an angle in degrees and then solve the formula ∆v=√2 sinꝋ∆ℎ. The result will be a very optimistic number that does not account for runway surface friction, angular momentum or excess thrust versus weight and drag, or a tailwind component.
The effect of slope steepness on resulting acceleration is non-linear. The tax on acceleration taken by steepness is a function of the sine of the angle, but the formula also has a multiplier of 2g and ultimately a square root. The resulting graph showing acceleration due to slope begins relatively flat, but quickly increases with the angle. At a 90-degree angle, it is equivalent to a 1g force of 9.8 N/Kg (Graph B).
This penalty/benefit of slope is non-linear and therefore asymmetric. In other words, the steeper the hill, the greater the benefit for taking off downhill and the greater the penalty for attempting an uphill takeoff. At some point in the incline, your aircraft will be at an angle where it only has enough thrust to hold its weight against the force of gravity. Beyond that, even at full power, the aircraft will start rolling backward.
An additional factor we haven’t discussed is the issue of aerodynamics, including lift drag and how much excess thrust is required to achieve breakaway lift.





I’d love to see how your analysis in this article compares to using the Performance Plus subscription on Foreflight (add a 1.5 safety factor) to figure our take-off and landing distance.